Lecture 10: Evolution as a combination of forces
Contents
Lecture 10: Evolution as a combination of forces¶
We’ve spent a bunch of time dissecting out the effects of individual forces on patterns of genetic variation within and among populations. In today’s lecture we’re going to take a step back from that and talk a bit about the big picture. We’re going to play with some of the ideas, and do some synthesis as to how this all fits together.
Adaptive Landscapes¶
R. A. Fisher’s Fundemental Theorem of Natural Selection is that populations will always be increasing in fitness. That is populations are constantly “climbing the hills” of their adaptive landscapes. How can this be? To examine this we’ll first drink the Kool-Aid, and delve in to the concept of adaptive landscapes, but later we’ll make fun of this concept a bit.
Sewall Wright actually came up with a similar idea as Fisher at roughly the same time. He figured this out by rearranging an equation we’ve seen before into a new form
The term \(\frac{d\bar{w}}{dp}\) is the derivative (slope) of the mean fitness as a function of the frequency of the \(A_1\) allele. This reformulation suggests allele frequency will always change in a way that will increase the mean fitness of a population. So in some sense, populations are always hill climbing. Can you imagine that this is true for more than a few generations? Why or why not? Also how would fitness that was determined by multiple loci effect this “Fundamental Theorem”?
Three allele sickle cell anemia: a human fitness landscape¶
What if all this time “we” have been lying to you about sickle cell anemia and actually there are 3 alleles? We wouldn’t do that, would we? Ahem… so assume there are actually 3 alleles at the sickle cell anemia locus. We’re going to add a third allele, the \(C\) allele which leads to the following genotype specific fitness table:
Genotype |
Absolute Fitness |
Phenotype |
|---|---|---|
\(AA\) |
0.9 |
malarial susceptibility |
\(AS\) |
1.0 |
malarial resistance |
\(SS\) |
0.2 |
anemia |
\(AC\) |
0.9 |
malarial susceptibility |
\(SC\) |
0.7 |
anemia |
\(CC\) |
1.3 |
malarial resistance |
So \(CC\) homozygotes are actually the most fit genotype. Here’s the rub- the \(C\) allele is actually super rare in the population. So rare in fact that no \(CC\) individuals are found (i.e. \(freq(C)^{2} \approx 0\)). As we had seen before the \(S\) allele is also relatively rare. This means that every \(C\) and \(S\) allele will be found in a heterozygous state, with the \(AS\) and \(AC\) being their predominant genotypes. Now take another look at the fitness table above- which heterozygote is more fit? How will selection act? Because \(AS\) heterozygote is more fit than \(AC\) heterozygote, \(S\) allele will rise in frequency, but \(C\) frequency will remain virtually unchanged. Even though \(CC\) homozygotes are the most fit genotype in this system, it is nearly impossible for selection to take us to that point in fitness space.
This is why it is often said that selection is “short-sighted.” Selection, due to the Fundamental Theorem is only trying to increase \(\bar{w}\) of a population, but because of that might lead to a local optimum in the fitness landscape and not the global optimum. Do populations ever get to global fitness optima? What other evolutionary forces might allow them to reach those points?
For Wright the answer was a combination of genetic drift and population structure. Let’s see this through the sickle cell anemia example before we formalize Wright’s idea. When the Bantu speaking peoples first arrived in West-Central Africa, they carried with them their tradition of slash and burn agriculture. This technique when coupled with the hot wet climate of the region, created nearly ideal growing conditions for the malarial parasite Plasmodium and its mosquito vector. So a population with the fitness table above was exposed to this new pathogen. The Bantu people settled in to small, rather isolated breeding groups in the area. Could this population structure actually help them?
Wright’s Shifting Balance Theory¶
Sewall Wright thought that population structure was the key for populations to get through fitness valley’s on their way to global fitness optimum in some landscape (see Figure 1 for an example).
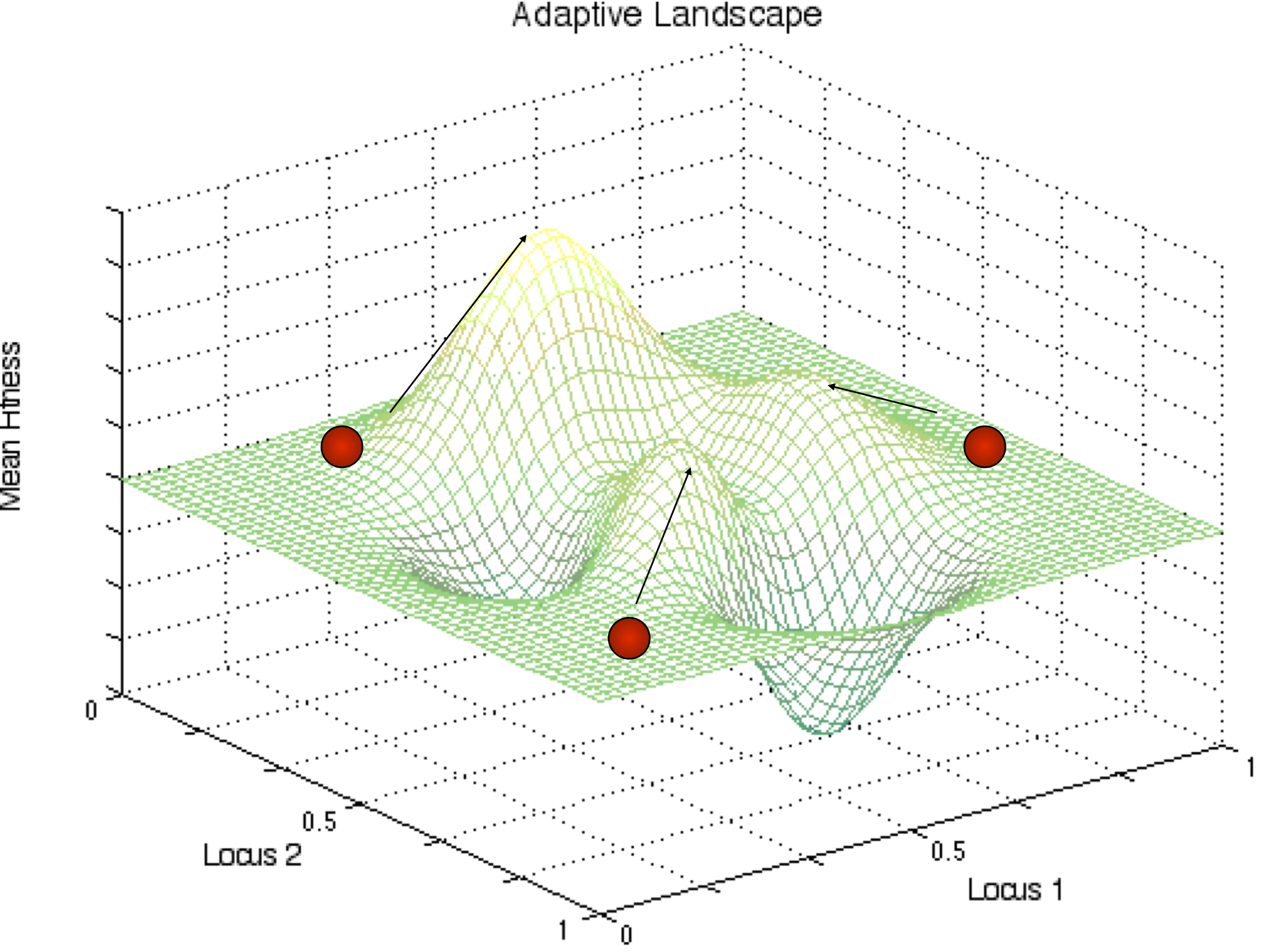
Fig. 11 Complex Fitness Landscape. Populations tend to always increase mean fitness due to the actions of natural selection. If this is so then initial conditions will determine which local optimum a population will go to. Sewall Wright believed that populations might be able to cross fitness valleys by drift in small populations. This Shifting Balance theory has been sharply criticized over the years.¶
In particular Wright felt that real populations should evolve under the joint influences of genetic drift and natural selection, because the majority of populations in nature actually show population structuring. He proposed a “shifting balance” of allele frequencies over time as a result of a “shifting balance” of the relative influences of drift versus selection as the main motive forces in evolution. This is the now (in)famous Shifting Balance Theory of evolution (a good critique of Wright’s idea can be found in Coyne, Barton, and Turelli (1997), Evolution 51:643-671).
Wright’s concept of the Shifting Balance is characterized by three phases of evolution:
Drift in local populations- populations drift to get near the domain of attraction of a local fitness peak.
Intrademic selection- selection within local populations drive those populations up fitness peaks.
Interdemic selection- migration from local populations in a manner proportional to mean fitness. Local populations on highest fitness peak swamp out rest of populations, raising \(\bar{w}\) of entire population.
So in essence Wright believes that neutral processes are needed at phases one and three, but selection is responsible at phase two. Fisher didn’t buy any of this and believed that mass selection alone was enough to get populations to global fitness peaks. In Fisher’s world view dominance itself might be able to be selected upon to help populations get through fitness peaks. Much of the empirical data these days say that Fisher was wrong about dominance, but Wright was wrong about the Shifting Balance Theory. Coyne et al. (1997) in particular point out that there is very little evidence to support Wright’s phase three of SBT, and moreover that the same impediments to peak crossing at phase one and two should actually hamper phase three (e.g. barriers to gene flow will still be present).
Fisher’s geometric model of adaptation¶
The example of Wright’s SBT puts in to context the idea of adaptation as a process that itself might be studied from a population genetic framework. How do populations climb peaks? What kinds of mutations are important? What is the distribution of mutational effects which fix as a population climbs some fitness surface? Fisher provided an extremely simply model of adaptation that allows one to ask all of these questions- this is what has come to be known as Fisher’s Geometric Model.
Fisher (think gray matter now) decided that one way to imagine the problem of organismal adaptation was as coordinates in some simple euclidean space. In a two dimensional setting we can imagine an organism’s fitness as a simple x,y point, with the optimal fitness of our landscape being at the origin (0,0). We then imagine that the environment has just changed so that current fitness is off of the optimum.
To watch the population evolve towards the optimum we can throw down mutations as random vectors (say random in direction and/or magnitude). We will then simply consider beneficial mutations (i.e. those that fix) to be vectors which carry our population closer to the origin. That’s it to the model. What’s really neat is that we can start getting serious results out of this model. Fisher noticed for instance that mutations of infinitesimally small effect (short vectors) should be about 50% beneficial, whereas large effect mutations should be overwhelmingly deleterious. This suggests that adaptation should proceed on average by small mutations! It also suggested to Fisher that treating phenotypic effects of individual genes/mutations as very small was perfectly reasonable and led to his pioneering work in quantitative genetics.
