Lecture 5: Introduction to Population Genetics

Lecture 5: Introduction to Population Genetics¶

What is Population Genetics?¶

Population genetics is primarily concerned with the genetic basis of evolution. Through a quantitative description of the dynamics of genetic variation within and between populations, population genetics has established both a descriptive and predictive understanding of how DNA, proteins, and genomes should differ among individuals. This leads to the ultimate definition of evolution- the change in the genetic makeup (allele and genotype frequencies) of a population over time.

Population genetics is distinct from nearly every other discipline in biology in that important results are often theoretical, rather than observational or experimental. The reason for this is that the object of study, changes in genotype frequencies and fitnesses over time, are very hard to observe in the lifetime of a human. If the relevant time frame for evolutionary change is on the order of hundreds of thousands or millions of years, than directly observing changes in genotypic frequencies is impossible. Instead, population geneticists rely on elegant mathematical models, first pioneered in the early part of the 20th century by Ronald Fisher, Sewall Wright, and J. B. S. Haldane, that describe the changes of genotype frequencies as a result of evolutionary forces. Progress is made by constructing population genetic models, examining their behavior, and looking to see if the state of populations is consistent with this behavior.

Fundamentally, genetic variation within populations is shaped by the combined actions of predictable, deterministic evolutionary forces and random, stochastic forces. The deterministic forces are sometimes referred to as “linear pressures” in that they tend to push allele frequencies in one direction (towards one, towards zero, or towards an intermediate frequency). Important forces of this nature are selection, mutation, gene flow, meiotic drive (unequal transmission of certain alleles [a form of selection]), nonrandom mating (also a form of selection). The primary stochastic evolutionary force is genetic drift (potentially) which is due to the random sampling of individuals (and genes) in finite populations. It is important to realize that the deterministic forces may act together or against one another (e.g., selection may “try” to eliminate an allele that is pushed into the population by recurrent mutation). Moreover, deterministic forces may act with or against genetic drift, to determine the frequencies of alleles and genotypes in populations (e.g., gene flow tends to homogenize different populations while drift tends to make them different). Hence, the interaction of these forces is what we are really interested in (a later lecture), but since this can get very complex mathematically, we will start by analyzing one force at a time.

Genotype and Allele Frequencies¶

To begin we need to understand some simple population genetic “bookkeeping.” Consider a locus with two alleles (alternative forms of the DNA sequence that “reside” at that locus, e.g., one from mother other from father). Now consider a population of N individuals (N=population size); this means that there are 2N alleles in the population. We can thus talk about genotype frequencies and allele frequencies. Let’s turn our attention to a hypothetical locus, the $A$ locus. We will first assume that there are two alleles segregating at the $A$ locus, $A_1$ and $A_2$. These could be two allozyme alleles (i.e. fast vs. slow) or two variant nucleotides at a polymorphic position in a genome (i.e. a SNP). Three genotypes are possible at the $A$ locus: two homozygous genotypes, $A_1A_1$ and $A_2A_2$, and one heterozygous genotype $A_1A_2$. We write the relative frequency of a genotype as $x_{ij}$ as this table shows:

Genotype:	$A_1A_1$	$A_1A_2$	$A_2A_2$
Relative Frequency:	$x_{11}$	$x_{12}$	$x_{22}$

As relative frequencies must add to one we have $$\begin{aligned} x_{11} + x_{12} + x_{22} = 1 \end{aligned}$$

The subscripting of the heterozygotes is of course arbitrary. Following my old advisor John Gillespie, we will take the convention of referring to the heterozygote as $x_{12}$ rather than $x_{21}$ – you can only use one subscripting convention if you want to keep things straight.

Often in population genetics we are interested in allele frequencies rather than genotype frequencies. The frequency of the $A_1$ allele in a population is simply

\[\begin{aligned} p = x_{11} + \frac{1}{2}x_{12}, \end{aligned}\]

and the frequency of the $A_2$ allele is

\[\begin{aligned} q = 1 - p = x_{22} + \frac{1}{2}x_{12}.\end{aligned}\]

There are two ways to think about $p$, the frequency of the $A_1$ allele. The first way is as the relative frequency of the $A_1$ allele among all of the (two) alleles at the $A$ locus in our population. This is simple enough to get one’s head around. The second way to think about $p$ is as the probability that an allele picked by random from the population is the $A_1$ allele. Picking an allele at random is actually composed of two parts, 1) picking a genotype at random from the population and 2) then picking an allele from that genotype at random. With our three genotypes at the $A$ locus we could write down $p$ as

\[\begin{aligned} p = (x_{11}\times1) + (x_{12}\times\frac{1}{2}) + (x_{22}\times0).\end{aligned}\]

This expression for $p$ is broken down into three terms which reveal the three mutually exclusive ways to sample an $A_1$ allele from the population and their associated probabilities. Let’s consider the first term in this sum. This represents the joint event where we sample an $A_1A_1$ individual from our population (this occurs with probability $x_{11}$) and then sample an $A_1$ allele from that individual (this occurs with probability one). In the second term we consider the joint event of sampling an $A_1A_2$ individual (with probability $x_{12}$) and then sampling an $A_1$ allele (with probability $\frac{1}{2}$). Now ask yourself, what is that zero doing in the third term?? Got it?

Let’s use a concrete example to drive this all home. Consider a population of $N = 100$ individuals. We observe the following number of genotypes at our $A$ locus:

Genotype:	$A_1A_1$	$A_1A_2$	$A_2A_2$
Observed Numbers:	25	50	25
Relative Frequencies:	0.25	0.50	0.25

The relative genotypic frequencies, the $x_{ij}s$, are simple to calculate, just divide the number of each observed genotype by the population size. For example, $x_{12} = \frac{50}{100} = 0.5$. Now let’s calculate allele frequencies. The allele frequency of the $A_1$ allele, $p$, is found in the following way

\[\begin{aligned} p = (0.25 \times 1) + (0.5 \times\frac{1}{2}) + (0.25\times0) = 0.5. \end{aligned}\]

So in this trivial example $p = q = 0.5$.

Let’s do a slightly less contrived example. Consider the following table of genotypes taken from screening African school children for the sickle cell anemia locus. In this case recall that $A_1A_1$ individuals are healthy, $A_2A_2$ individuals are sick, and heterozygotes show increased resistance to malaria.

Genotype:	$A_1A_1$	$A_1A_2$	$A_2A_2$
Observed Numbers:	411	1404	185
Relative Frequencies:	0.2055	0.702	0.0925

First double check that I have gotten relative genotypic frequencies correct. Next calculate the allele frequencies. I get $p = 0.556$, what do you get?

The Hardy-Weinberg Law¶

Perhaps the best known population genetic model is the famous Hardy-Weinberg law, which describes the relationship between allele and genotype frequencies at an autosomal locus in an equilibrium randomly mating population. By equilibrium we mean a population that is not undergoing evolutionary forces such as selection, mutation, or genetic drift. By randomly mating we mean that individuals mate with each other irrespective of relatedness or geography. Populations where cousins mate are not randomly mating- this is called inbreeding. Populations where $A_1A_1$ individuals are more likely to mate with other $A_1A_1$ individuals are not randomly mating- we call this assortative mating. Similarly if one is more likely to mate with their neighbors, geographically, than this too is not random mating.

The easiest way to envision an honest to goodness Hardy-Weinberg population is as hermaphrodite, broadcast spawners, something like sponges or corals. Individuals produce both sperm and eggs, and randomly let them go into the environment to meet up and form zygotes. In this way the probability of forming an $A_1A_1$ zygote is the product of the probability of choosing an $A_1$ egg, $p$, and the probability of choosing an $A_1$ sperm (these probabilities are identical because of our assumption of hermaphrodites). Thus the probability of randomly forming an $A_1A_1$ zygote is $p^2$. By similar reasoning, the probability of forming an $A_2A_2$ zygote is $q^2$. There are two ways to form an $A_1A_2$ heterozygote. The first way is with an $A_1$ sperm and an $A_2$ egg. This probability is $pq$. The second way would be with an $A_2$ sperm and an $A_1$ egg. Again, this probability is $pq$. Because we sum mutually exclusive probabilities, the total probability of randomly forming a heterozygote is $2pq$. Congratulations, you’ve just derived your first population genetic model.

After one round of random mating the frequencies of the three genotypes at our locus are

Genotype:	$A_1A_1$	$A_1A_2$	$A_2A_2$
H-W Frequency:	$p^2$	$2pq$	$q^2$

These are the Hardy-Weinberg genotype frequencies. They only depend on allele frequencies, thus if you know $p$ you know all of the genotype frequencies.

A couple of things to note about random mating in our diploid hermaphrodites:\

Allele frequencies are unaffected by random mating. Random mating can change genotype frequencies, but not allele frequencies, thus after one round of mating Hardy-Weinberg genotype frequencies will remain unchanged, forever!

2) In our diploid hermaphrodites it only takes one generation to achieve H-W equilibrium proportions. In species with separate sexes it takes two generations.

3) To come up with genotype frequencies after random mating we only need to know allele frequencies before random mating, not genotype frequencies.

Let’s step back to our numerical example from human sickle cell anemia. Our goal will be to predict Hardy-Weinberg expected values for genotype frequencies at this locus, given our observed allele frequencies. We have already done the first step which is to calculate the frequency of the $A_1$ allele, in this case $p = 0.556$. Now lets calculate the frequency of the $A_2$ allele, $q = 1 - p = 1 - 0.556 = 0.444$. Using these allele frequencies we can fill out a table of genotype frequencies

Genotype:	$A_1A_1$	$A_1A_2$	$A_2A_2$
H-W Frequency:	$p^2$	$2pq$	$q^2$
H-W Expected Frequencies:	0.309	0.494	0.197
Observed Frequencies:	0.2055	0.702	0.0925

Compare the observed genotypic frequencies with what we would expect from the Hardy-Weinberg law. Pretty different, huh? In particular I want you to notice how we observe many more heterozygotes than we would expect. This is what is called in the business an excess of heterozygotes. Why are we seeing this difference? Which of our Hardy-Weinberg assumptions have failed us? One can always test for a significant deviation from our H-W expectation using a chi-square statistic.

So what happens in species with separate sexes (dioecious species)? What if genotype frequencies are different between the sexes? At the most extreme, lets imagine that all males are $A_1A_1$ and all females are $A_2A_2$. With an equal sex ratio the frequency of the $A_1$ allele is $p=0.5$. In this case, after one round of random mating every individual in the population is $A_1A_2$, and the frequencies of the heterozygotes is one. This is clearly far from the Hardy-Weinberg expected genotype frequencies. However, after just one more round of random mating the frequencies of the $A_1A_1$, $A_1A_2$, and $A_2A_2$ genotypes are returned to their Hardy-Weinberg values of $\frac{1}{4},\frac{1}{2}$, and $\frac{1}{4}$. So even for dioecious species with very different allele frequencies it only takes two rounds of random mating to get back our H-W expected genotype frequencies.

Heterozygosity¶

As we talked about in the last lecture, getting a handle on the amounts of genetic variation within a population is very important both to genetics and evolutionary theory. One broad way to describe the “amount” of variation that exists at the genetic level is to describe a population by the probability of sampling a heterozygous genotype from it. For obvious reasons we call this measure the heterozygosity of a population.

Our cursory look at the Hardy-Weinberg law suggests that heterozygosity might depend on allele frequencies. Figure 1 shows a plot of the frequency of heterozygotes as a function of the $A_1$ allele frequency under Hardy-Weinberg conditions. Ask yourself this simple question- at what allele frequency is the probability of sampling a heterozygote from a population maximized? Does this make intuitive sense to you?

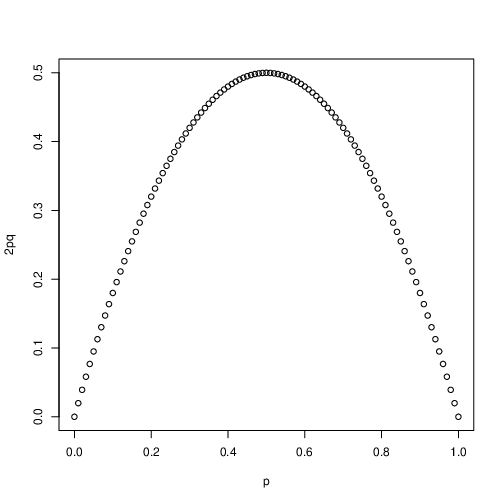
Fig. 5 The frequency of heterozygotes as a function of allele frequency in H-W equilibrium populations¶

Before moving on to a formal treatment of heterozygosity, let’s first generalize the Hardy-Weinberg law to the case where we have more than two alleles at a locus. Good examples of such loci in actual genomes would include microsatellites or allozyme polymorphisms, as opposed to SNPs which tend to be diallelic. If we have $k$ alleles at a locus, $A_i$, $i=1...k$, let their frequencies be called $p_i$, $i=1...k$. It follows that the frequency of the $A_iA_i$ homozygote after random mating should be $p_{i}^2$ and the frequency of the $A_iA_j$ heterozygote should be $2p_ip_j$. Simple enough, but make sure this is straight in your head. It might be helpful to write out the three allele example in its entirety at this point. Moving on, the total frequency of homozygotes in our population is

\[\begin{aligned} G = \sum_{i=i}^{k}p_{i}^2. \end{aligned}\]

$G$ here is called the homozygosity of a locus. Ask yourself- what is the probabilistic interpretation of $G$? The heterozygosity of a locus is the complement (in probability space) of homozygosity

\[\begin{aligned} H = 1 - G = 1 - \sum_{i=i}^{k}p_{i}^2. \end{aligned}\]

For populations that obey the assumptions of the Hardy-Weinberg law, heterozygosity will actually equal the frequency of heterozygotes, however heterozygosity is calculated using only allele frequencies. Because of this heterozygosity is often used to describe populations that don’t conform to H-W assumptions. In many ways it’s just a convenient measure- like temperature.

Lecture 4: Genotypic and Phenotypic Variation

Lecture 6: Natural Selection I: Adaptation

Bio 380-- Evolutionary Biology